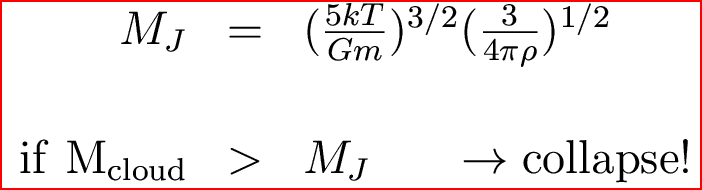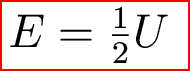
Start with the virial theorem -- remember that, from our discussion of the Sun? The virial theorem describes a system in equilibrium. If the total energy of a system is E and the gravitational potential energy is U, the virial theorem says that
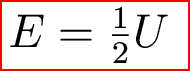
But remember that total energy is the sum of potential energy (U) plus kinetic energy (K). So we can rewrite the virial theorem as
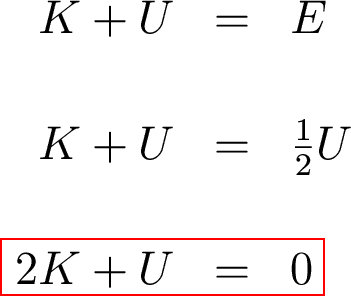
So how does this apply to gas clouds?
What is K, the kinetic energy? In gas clouds, the kinetic energy is due to the motions of the atoms which make up the cloud, so if there are N total atoms in the cloud the kinetic energy is
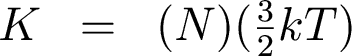
And remember that the gravitational potential energy is given by
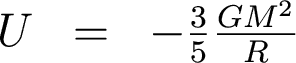
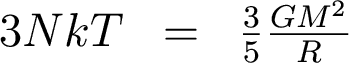
Now what?
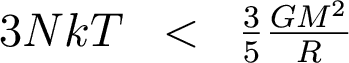
So let's substitute. The number of particles is simply the mass of the cloud divided by the mass per particle:
Assuming the cloud has a constant density rho, the size of the cloud can be related to the mass and density by
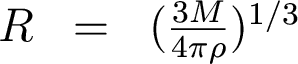
Plugging these numbers into the collapse criterion equation and doing some math, we get the condition for collapse:
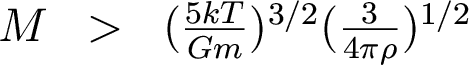
Call this number the Jean's mass, then we can say the cloud will collapse if its mass is bigger than the Jean's mass. This is called the Jean's criterion: