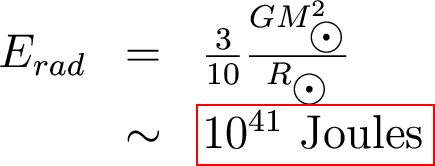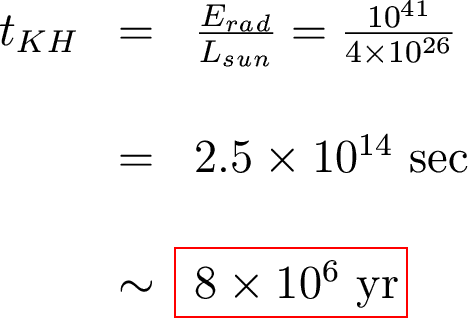
Could the Sun's gravitational potential energy be powering
the Sun?
How much potential energy
does the Sun have?
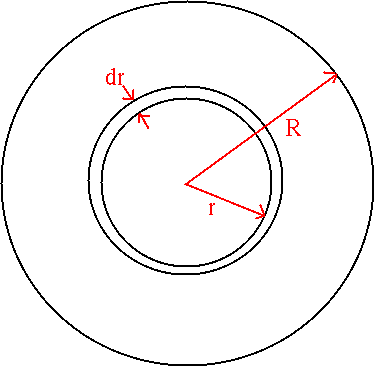
Consider a sphere of radius R, made up of mass shells with thickness dr:

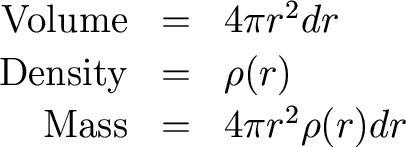
So each shell has gravitational potential energy

Now, let's make the Homeresque assumption that density is constant. Then
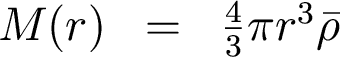
And we get the following expression for the gravitational potential energy of each shell:
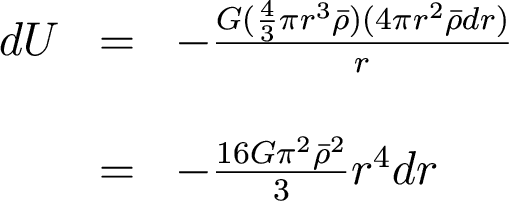
If we now integrate over all radii, we get the gravitational potential energy of the whole sphere:
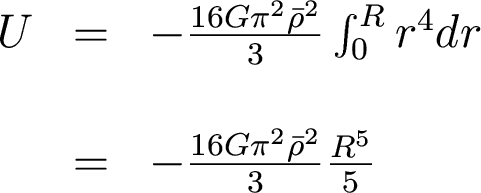
And if we remember that
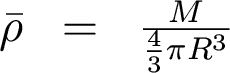
We can get the gravitational potential energy of a uniform sphere
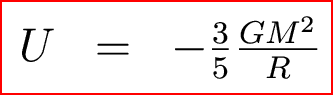
Notice that as R gets smaller, U gets more negative --
energy is being converted to other forms, like heat. If the Sun can radiate
this heat into space, then gravitational contraction might produce the
luminosity of the sun.
How much of this gravitational energy can be radiated away?
A side trip: The Virial Theorem: 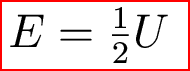
Really? Yep, for example: circular orbits.
But back to the contracting Sun. The virial theorem says that half the change in gravitational energy stays with the star (it heats the star). The other half is radiated away.
So, let's say that the Sun has been contracting and was
originally much, much bigger.
Initially its gravitational potential energy was tiny
(why?), so the change in gravitational
energy is
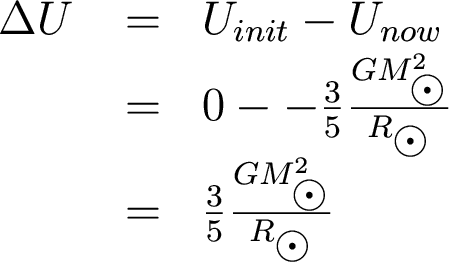
Now, half of this energy could have been radiated as the Sun shrank: