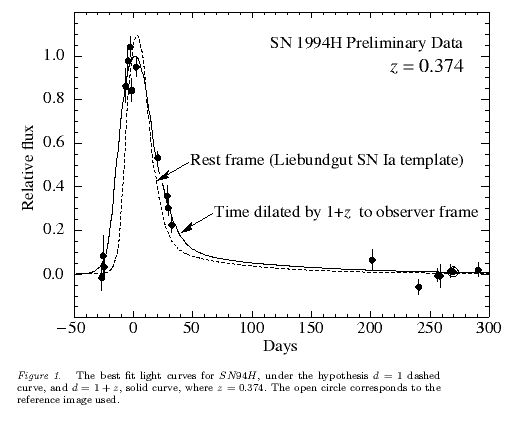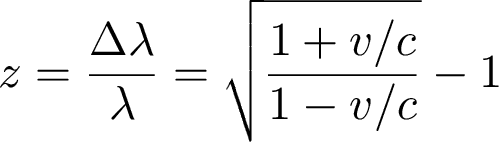
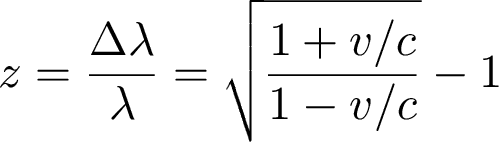
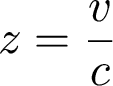
The cosmological redshift is something different, although we are often sloppy and refer to it in the same terms of the doppler redshift. The cosmological redshift is actually due to the expansion of space itself.
How do we relate the cosmological redshift to the expansion of the Universe? Start with the R-W metric again
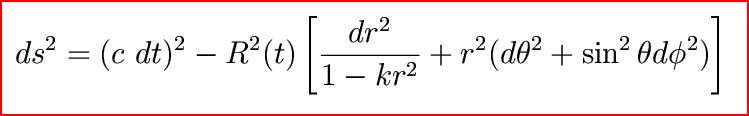
and watch what happens to a light ray moving through space. In this case, ds2=0 (why?)
Again orient the coordinate system so
that
theta=phi=0,
then integrate along the path length, from the time of emission (te)
to now (t0). Look at two wavecrests
in the light ray, separated in time by ![]() .
.
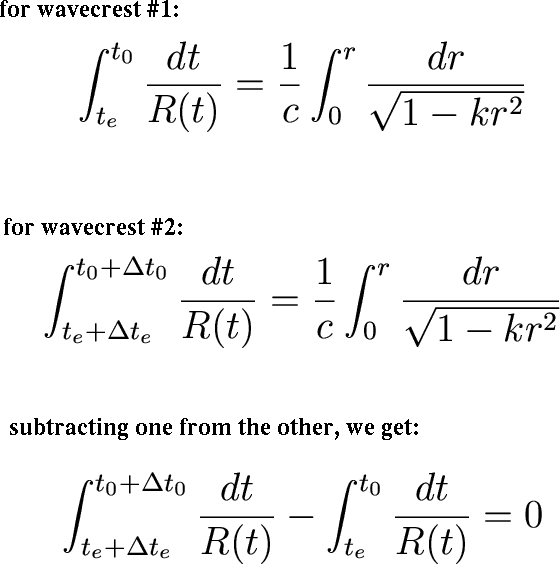
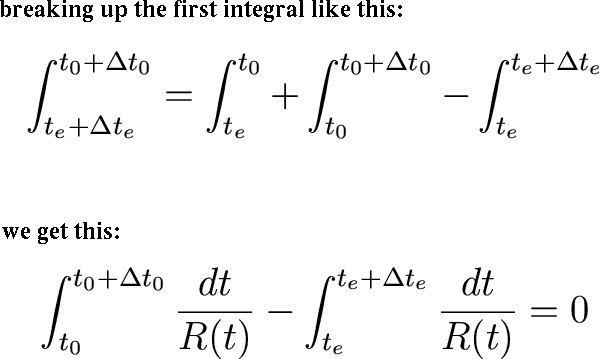
(sheesh!)
Okay, now we can pull R(t) out of the integral and treat it as a constant (why?). Then we get
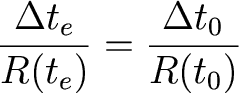
Now since wavelength is equal to c![]() we have
we have
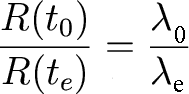
Or, by our definition of
redshift: 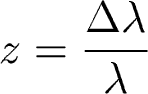
We get:
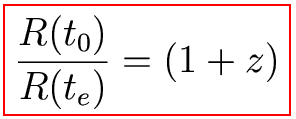
So redshift is related to the
expansion factor of
the
Universe. If we measure a redshift of z=2, the Universe is 3x
bigger
now than it was when that photon was emitted.
Also, this gives rise to an expression of cosmological time
dilation: