Spacetime Metrics

A metric defines the distance between two points.

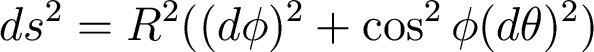
Example: Cartesian planar coordinates (x₁,y₁) & (x₂,y₂). The metric defining the distance between these points is simply given by

ds²=dx²+dy²

In spacetime we can define an event as something marked by the 4 coordinates x, y, z, and t. (Note that an event may be uneventful.)

What is the metric defining the distance between two events? Here's one in Euclidian geometry, from special relativity:

ds²=(c dt)² - (dx² + dy² + dz²)

This metric has the advantage of being invariant under a Lorentz transformation -- that is, observers in different inertial frames will all measure the same interval ds.

Note that, unlike spatial intervals, the spacetime interval ds² can be positive, negative, or zero. What does this mean?

positive: time-like intervals, events which are causally connected.

zero: light-like intervals, only something travelling at the speed of light can link the events.

negative: space-like intervals, events which are not causally connected. Unknowable.

But who says the spatial geometry is Euclidian? It seems to be on small scales, but what about on the largest scales? Remember what general relativity says: spacetime can be curved.

Take another two dimensional example: the surface of a sphere. If points on a sphere of radius R are marked by coordinates theta and phi, the spatial distance between them is given by

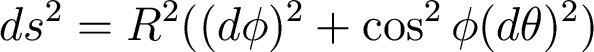
This metric is different than the one for euclidian geometry -- the distance between two events depends on the curvature of spacetime.

Keep thinking about two dimensional surfaces.

positive curvature (a ball): parallel lines eventually meet

zero curvature (flat paper): parallel lines remain parallel

negative curvature (a saddle): parallel lines diverge

(courtesy Syracuse University)

Unfortunately, it is much harder to visualize the extension of this analogy into curved three dimensional space. Nonetheless it is an extremely useful analogy which we will often return to.

Question: How does the volume of space differ at large distances for different spacetime curvatures? How could we test this?

The Robertson-Walker Metric

Let's go back to the cosmological principle: the universe is homogeneous and isotropic.

We need a metric that reflects this -- it must be invariant under translations (homogeneous) and under rotations (isotropic). Only three possibilities exist, and they are all contained in the most general form of the spacetime metric (derived in 1934): the Robertson-Walker metric.

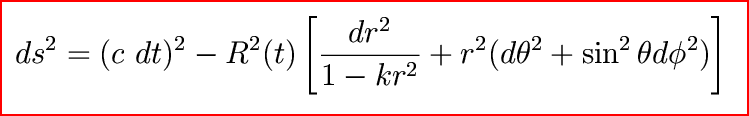
What is all this?

R(t): scale factor of the universe. R(today)=1

k: curvature of spacetime

+1: positive curvature

0: flat space

-1: negative curvature

r, theta, phi: comoving coordinates

What do we mean by comoving coordinates?

Comoving coordinates are coordinates that move along with the overall expansion of the universe.
Imagine a distant galaxy. It is located at the coordinate (r,theta,phi). As long as no force acts on it, it will always be at that coordinate.

Its true distance does change, and is given by R(t) times the comoving distance (=Rr in a flat universe). But the change in the true distance is completely described by the change in the expansion factor R(t).

What could cause a galaxy to change its comoving coordinate?