When did ellipticals form - clues from low-moderate redshift

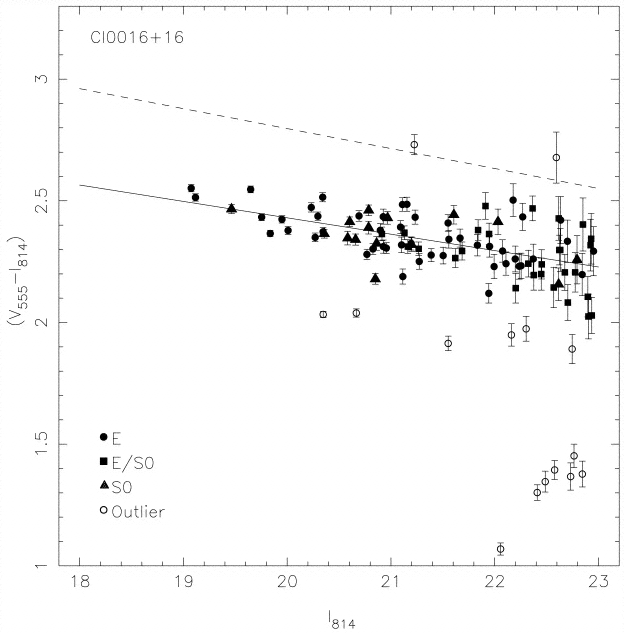
Ellipticals follow a well defined color-magnitude (cm) relationship. Look at Coma and Virgo. This relationship is due to metallicity: more massive galaxies are more metal-rich, and therefore have redder stars. But there is scatter in the relationship: due to differences in ages, perhaps? Bower etal 1992 show that the scatter in the cm relationship is < 0.04 magnitudes in Coma and Virgo. Think: if all E's formed at the same time, there would be no scatter in the cm relationship. if they formed randomly, there would be lots of scatter. So the scatter tells us how synchronized E formation was. How can we quantify this?	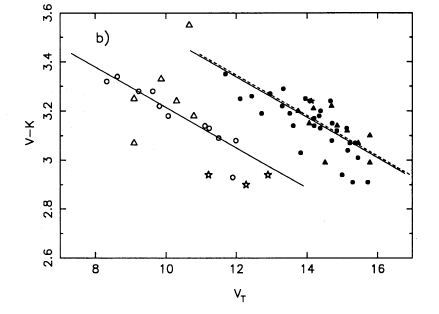(from Bower etal 1992)
Imagine a single burst of star formation evolving with time. The scatter in the cm relationship depends on: spread in formation age rate at which the population gets redder as it ages when you observe the population where beta is a synchronization parameter: "pure synchronization" : beta=0 "random formation": beta=1
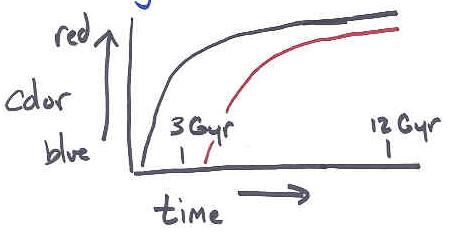
so at z=0, delta< 0.04 (Bower etal 1992). then we have dC/dt from models, and constrain a combination of beta and delta t (=tobs-tform). For the Bower etal data If no synchronization (beta=1): formation time > 13 Gyr ago If synchronized (beta=0.1): formation time > 7 Gyr ago.

Going to higher redshift

Ellis etal 1997 used HST to look at three different z ~ 0.5 clusters. They found a cm relationship scatter of delta < 0.07. A similar analysis gives tobs - tform ~ 5 Gyr unless formation is highly synchronized (in three different clusters?). in LCDM universe, z=0.5 means tobs=8.4 Gyr, so tform = 3.4 Gyr, or zform>=2.	(from Ellis etal 1997, ApJ, 483, 582)