Astr 222 Practice Midterm #1 Answers
Short Answer
- Describe what is meant by Population I
objects and Population II objects. Give examples.
Good
answer: Population I and II refers to different
stellar populations in our Galaxy, and was coined by Walter
Baade in the 1940s. Population II objects are older,
metal-poor stars and globular clusters like those found in
the Galaxy's halo. Population I refers to more
metal-rich objects like disk stars, the Sun, or young open
star clusters.
Weak answer:
Populations II stars are old stars, while the Sun is a
Population I star.
- Describe the Magellenic Clouds.
Good answer: The
Magellenic Clouds are two dwarf irregular galaxies in the
Milky Way's halo. They are gas-rich and actively forming
stars. They are small (kpc or smaller) and low mass (a few
percent or less of the Galaxy's mass) and lie ~ 50-60 kpc
away. They are interacting with one another and also
orbiting our Galaxy with a period of a few billion years.
Weak answer: The Magellenic Clouds are dwarf galaxies
that orbit the Milky Way.
- Why do we believe there is a lot of dark
matter in the galaxy?
Good answer: If we
look at the rotation curve of the Galaxy -- the orbital
speed as a function of radius -- we find that the rotation
curve stays flat well beyond the point where there are no
more stars. Since V2 ~ GM/R, M ~ RV2/G
so that if the rotation curve is flat there must be more and
more mass in the Galaxy as we go to large radius. But since
we have run out of stars and gas at those distances, that
mass can't be due to normal stars and gas -- it must be
"dark matter."
Weak answer: The galaxy rotates too fast to be held
together by the stars' gravity alone.
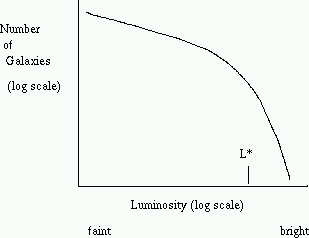
- Describe what is meant by the "luminosity
function" of galaxies. In this context, what is L*? Sketch
what this function looks like.
Good
answer: luminosity function describes the
relative numbers of galaxies of different luminosities --
i.e., how many bright galaxies, how many faint galaxies.
There are a lot more faint galaxies than bright ones. L*
is the galaxy luminosity above which the number of
galaxies drops exponentially, and is about 2x1010
Lsun. For galaxies fainter than L*, the luminosity
function rises like a power law as you go fainter and
fainter, meaning that there are many many more galaxies at
fainter luminosity. Here is a sketch:
Weak answer:
The luminosity function tells you how many bright galaxies
there are are. (no sketch, or unlabelled sketch)
- Why does the X-ray variability of the galactic
center place a limit on the size of the object at the center?
Good answer: In
order for the light output of an object to vary appreciably,
it must coordinate itself so that the entire object varies
its light output coherently. In other words, one side needs
to know what the other is doing, so they can both "get
bright" or fade. But the fastest that information (ie "time
to get bright!") can be conveyed from one side to the other
is at the speed of light, and that takes a time t=R/c. So if
an object varies over a time t, it must have a size which is
no larger than ct.
Weak answer: Big things cannot change their
brightness quickly.
Numerical Problem
- You are studying a distant star cluster, and
find that the stars appear too red for their spectral type --
their colors are too red by 0.25 in B-V color. You also find
that there is a Cepheid variable star in this cluster, with a
period of 10 days and a mean apparent V magnitude of 7.0. How
far away is the cluster?
If the stars are "too red"
by 0.25, that means E(B-V)=0.25. But since AV=3.2E(B-V),
stars which are too red by 0.25 are extincted by
3.2x0.25=0.8 magnitudes. So if we correct for dust, the mean
apparent V magnitude is actually 6.2 (ie 7.0-0.8). If the
Cepheid has a period of 10 days, then it has an mean
absolute magnitude of M=-2.8xlog(10)-1.43=-4.23. Then we can
get distance from m-M=5logd-5, so 6.2-(-4.23)=5logd-5, or
d=1200 pc.
- If your telescope can reliably measure the
brightnesses of stars down to 20th magnitude, what is the
fathest away you could detect a Cepheid variable? Remember
that the most luminous Cepheids have period of about 100 days.
If a luminous Cepheid has
a period of 100 days, it has an absolute magnitude of -7.0.
If you detect them down to 20th magnitude, that means
m-M=20-(-7)=27, or a distance of d=2.5 million parsecs
(Mpc). And yes, we have measured Cepheids out that far (and
farther)!
Essay
Sorry, no answers to the essay
questions, since one of them will be on the exam!