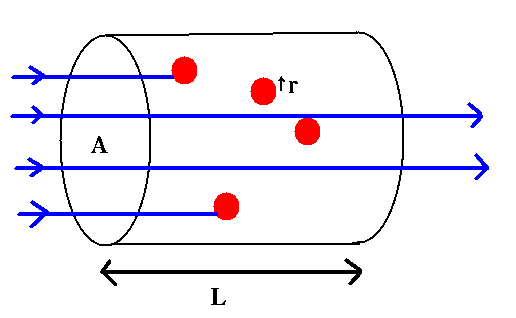
A: area of the cylinder's end
L: length of the cylinder
r: size of absorbers
n: number density of absorbers
Optical depth describes how much absorption occurs when light
travels through an absorbing medium (for example, a planetary atmosphere
or a interstellar dust cloud).
Think about light rays passing through a cylinder of absorbers:

A: area of the cylinder's end
L: length of the cylinder
r: size of absorbers
n: number density of absorbers
We can define a cross-section for the absorbers as
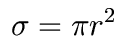
Then,
As long as the absorbers don't shadow each other, the fractional area blocked is
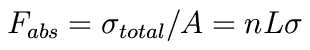
We refer to this as the optical depth:
If the optical depth is large, we say the region is optically thick -- light is readily absorbed. If the optical depth is small, the region is optically thin, and light passes through easily.
Often, we will also talk about the column density (aka surface density) of material. Imagine squashing that cylinder along its axis. Then the number of absorbers per unit surface area is given by the column density:
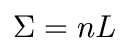
Note that the absorbing cross section of atoms varies strongly with wavelength, so that the optical depth varies strongly with wavelength.
We said that the optical depth was the fraction of the light
absorbed, as long as the absorbers don't shadow one another. If there are
lots of absorbers (ie region is very optically thick), this definition breaks
down. We need to do things a bit more carefully here.
Think of an optically thick layer as a bunch of optically thin layers all stacked together:
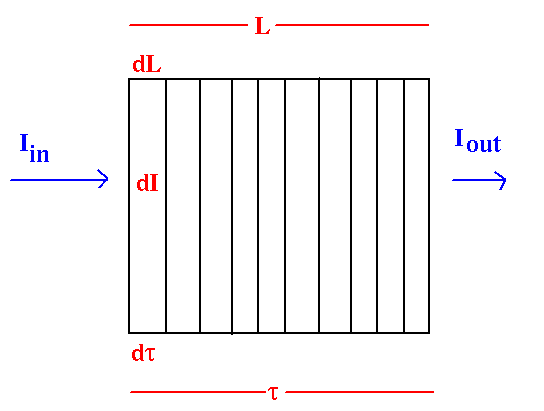
In each optically thin layer, the change in radiation intensity, dI, is simply equal to the intensity coming in times the optical depth of that layer:
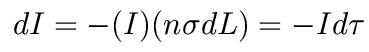
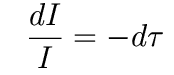
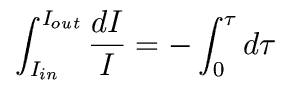
This integrates to
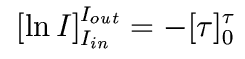
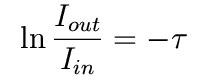
In other words,
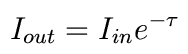
So as optical depth gets large, the amount of light drops exponentially.
If we go back to the optically thin case,
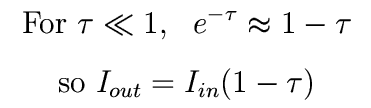
we see again that tau is the fraction absorbed, so the expression holds for any optical depth.
Question: How large must the optical depth be in order to absorb