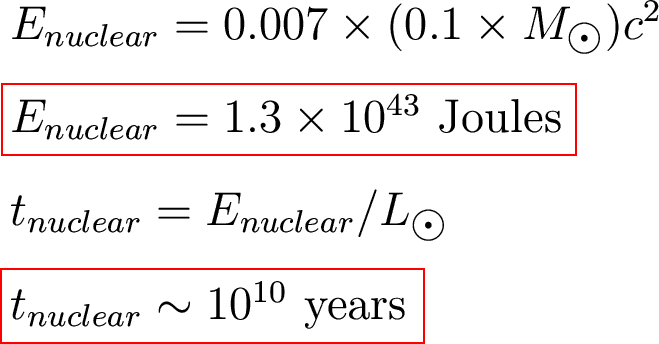Nuclear Reactions

So if gravity can't power the sun, how about processes inside an atom? We have two choices here:

1. Chemical reactions (ie reactions dealing with atomic bonds between atoms and electrons)

Typical energy per atom of around 10 electron volts (the amount of energy stored in the atomic levels of hydrogen and helium).
Not enough energy to power the Sun for very long (less than gravity!)

2. Nuclear reactions (reactions between atomic nuclei)

Typical energies are millions of times larger than for chemical reactions.
Lots of energy available!

So time for a little NUCLEAR PHYSICS (woo-hoo!)

Inside the Atom

Let's look at Hydrogen and Helium (98% of the Sun)

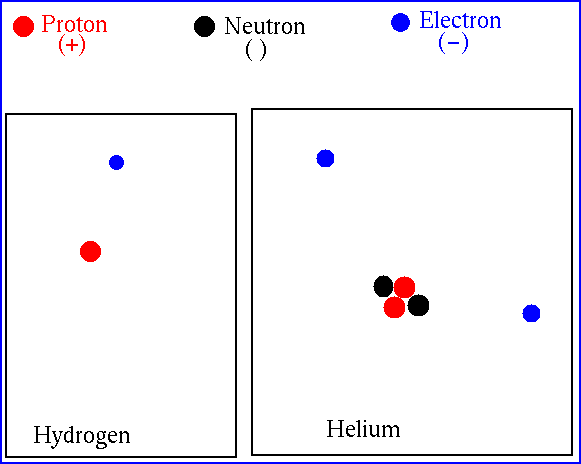At the center of the Sun, the temperature is high enough that Hydrogen and Helium (and just about everything else) is ionized -- the electrons are no longer bound (attached) to the atoms. We just deal with bare nuclei.

Let's do a few definitions to make life easier.
First define the atomic mass unit as being 1/12 of the mass of the carbon-12 atom:

1 AMU = 1.660540x10^-27 kg Next, bring

Einstein into the picture. Einstein realized that E=mc². Mass and energy are equivalent, related by the speed of light, c.

So we can also talk about mass in terms of energy:

1 AMU =~ 931.5 million electron Volts (MeV) (where 1 eV = 1.6x10^-19 Joules)

Okay, now how does ionization work? If we add energy to the atom, we break apart the electron from the proton. Let's look at this from a mass perspective.

Since a hydrogen atom is simply a proton plus and electron, the mass of the hydrogen atom should simply be equal to the mass if the proton plus the mass of the electron, right?

Wrong! M(hydrogen) - M(proton) - M(electron) = -13.6 eV

What? What is this energy difference? It is the binding energy of the hydrogen atom.

In other words the correct (schematic) equation is not

hydrogen = proton + electron

But rather

hydrogen + energy = proton + electron

What about nuclear processes?
Instead of ionizing atoms, let's look at fusing atoms together.

A hydrogen nucleus is simply a proton.
A helium nucleus is two protons and two neutrons.

We can make helium by fusing together 4 hydrogen atoms. But look:

4 x M(hydrogen) - M(helium) = 26.71 MeV. Compare this to what happened when we ionized hydrogen:

The energy difference is MeVs, not eVs. Much bigger.
The energy left over is positive: energy is produced.

So this time our schematic equation is
hydrogen + hydrogen + hydrogen + hydrogen = helium + energy So every time you fuse 4 hydrogen atoms together to make helium, 26.7 MeV is released. This is equivalent to about 0.7% of the mass of the 4 original hydrogen atoms.

But is it enough to power the Sun?

Let's estimate how long the Sun could shine by fusing hydrogen into helium.

Assume

The Sun was originally 100% hydrogen.
The Sun can only convert the inner 10% into helium.

How much energy is that?

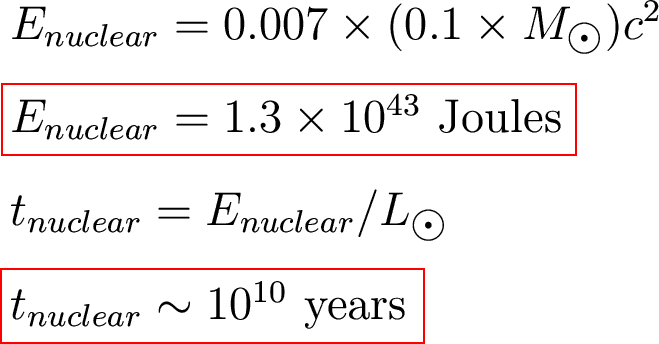Oooh, now we're cooking...

Nothing is free -- what's the problem with fusing hydrogen nuclei?

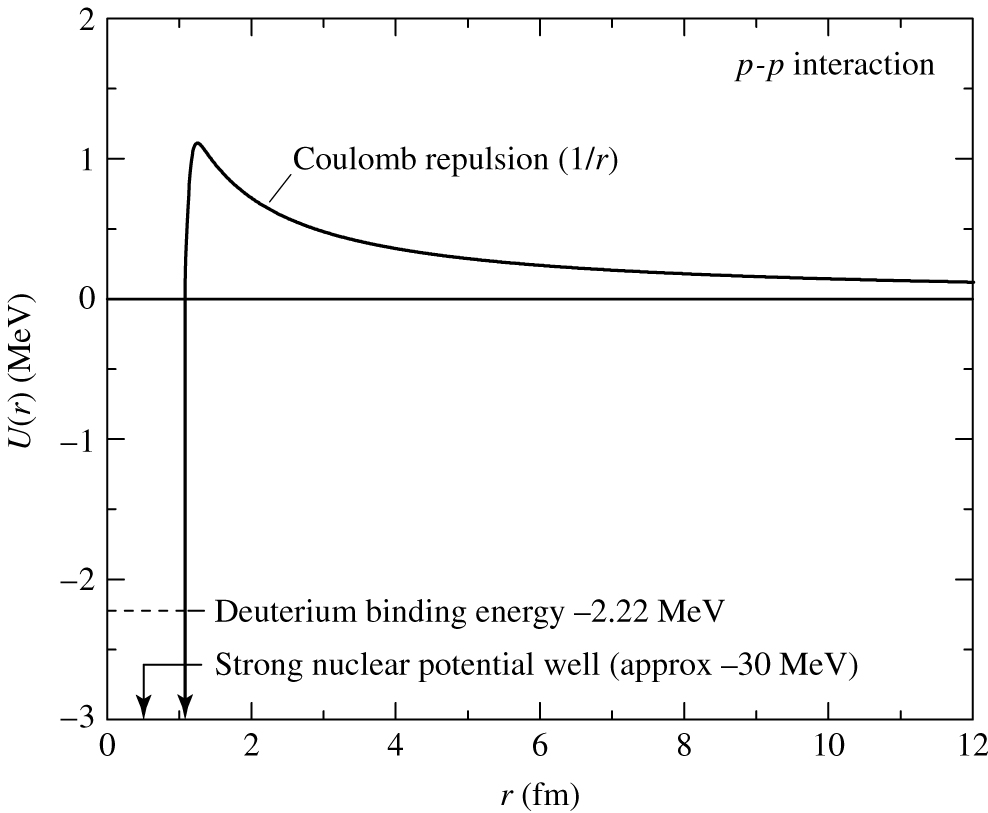
There are two forces acting inside atoms:

The electromagnetic force

Long range
Coulomb repulsion/attraction

The strong nuclear force

Very short range
Holds the nucleons (protons + neutrons) together

(what are the other two fundamental forces?)

Protons have positive charge. Like charges repel -- the electromagnetic force.
We need to overcome this repulsion to have the nuclei fuse.

How do we do this? Energetic nuclei! How do we make energetic nuclei?