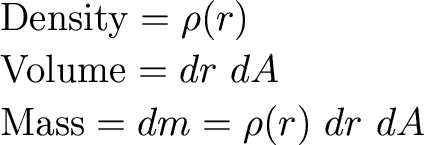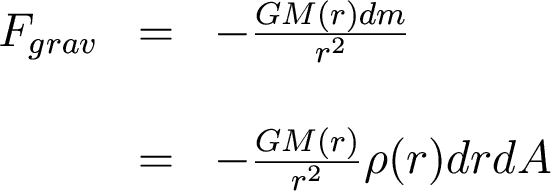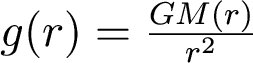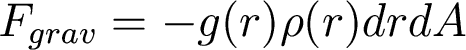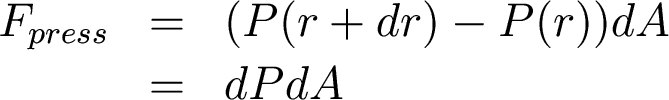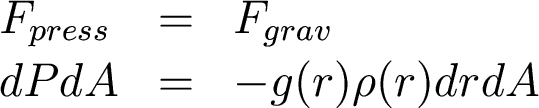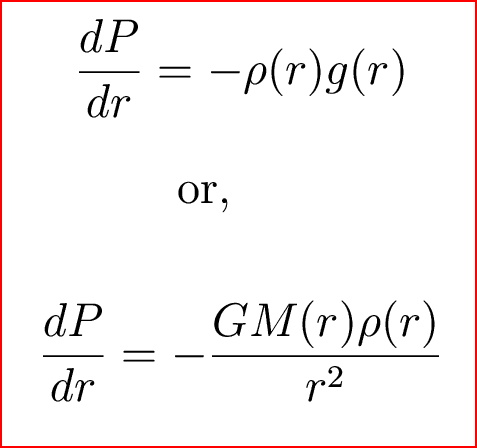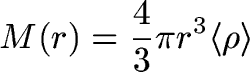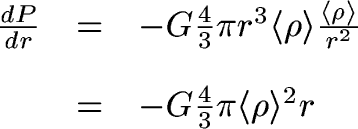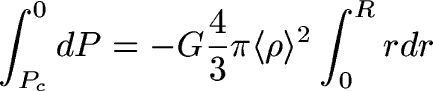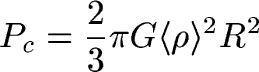Hydrostatic Equilibrium
Consider a cylindrical region (length dr, end area dA)
at a distance r from the center of the
Earth:
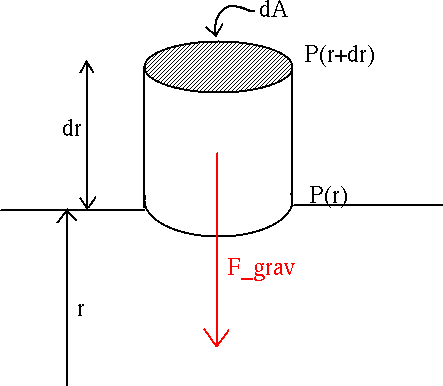
And the cylinder has properties
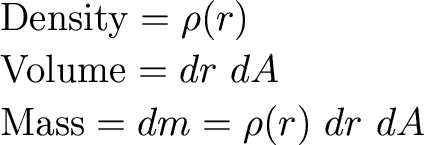 Now, what is the force of
gravity acting on the cylinder?
Now, what is the force of
gravity acting on the cylinder?
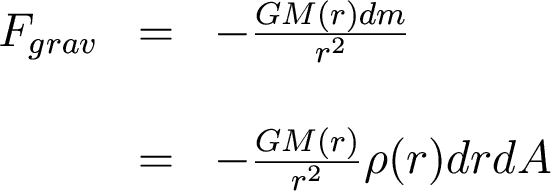
Now, define the quantity
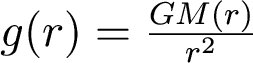 (what is g(r)?)
(what is g(r)?)
so that we have
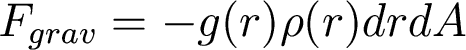
What balances this gravitational force? Pressure. So let's calculate the pressure acting
on the cylinder. (remember Pressure = Force/Area)
The cylinder feels the pressure from
the stuff above it pushing down, plus the pressure from the
stuff below pressing up. So the net pressure is
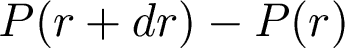
and the force associated with this pressure is
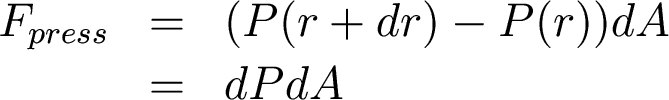
OK. These forces must balance for the sun to be in equilibrium:
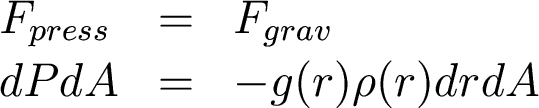 A little algebra yields The Equation
of Hydrostatic Equilibrium:
A little algebra yields The Equation
of Hydrostatic Equilibrium:
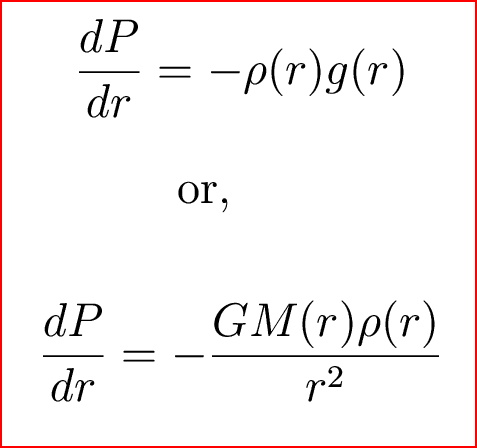
Estimating the central pressure
of the Earth
First, let's assume the density of the Earth does not change with radius.
Then we can express M(r) for the Earth as:
So that the equation of hydrostatic equilibrium becomes:
Now, let's integrate this from the center of the Earth to the surface:
To end up with an expression for the pressure at the center of
the Earth:
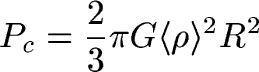
Numbers:
- G = 6.67x10-11 N m2 kg-2
- average density of Earth = 5500 kg m-3
- radius of Earth = 6400 km = 6.4x106 m
So plugging in, we get Pc = 1.7x1011 N m-2
= 1.7x106 atmospheres