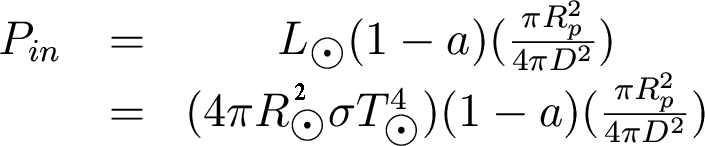
Equilibrium Temperatures of Planets

What is the equilibrium temperature of a planet? What do we mean by equilibrium?

Consider a planet of size R_p at a distance D from the Sun. Define the albedo (a) of a planet to be the fraction of incoming energy that is reflected off the planet (albedo can be as small as 0, or as large as 1). Question: How does albedo relate to the amount of energy absorbed by a planet?

With this definition, the amount of energy a planet receives from the Sun every second is given by

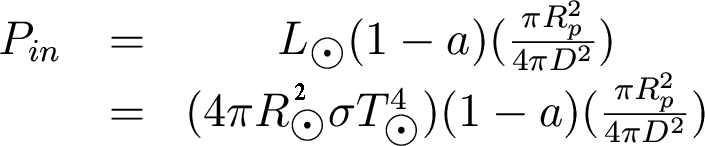
Now, how much energy is the planet giving off each second (not reflecting, but actually emitting)?

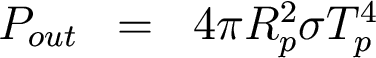
In thermal equilibrium, these rates are in balance:

Question: What happens if we are not in thermal equilibrium?

Equating these two rates and doing some algebra, we find that

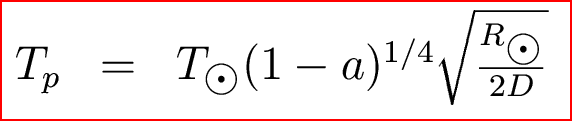
Note the dependencies, and that T_p does not depend on R_p. Why??

Let's try this for Venus. Putting in the numbers (a=0.6, T_sun=5770K, R_sun=7x10⁵ km, D=0.72 AU) we get the equilibrium temperature of Venus = 260 K.

The surface temperature of Venus = 740 K. Whoa! Where'd we mess up??

For that matter, the equilibrium temperature of the Earth is 255 K (or ~ -1 F). Something's wrong!