Gravitational Collapse

So we have lots of gas in the interstellar medium. What are the properties of these clouds?

	Diffuse HI Cloud	Molecular Cloud Core
Temperature	50 K	150 K
Density	500 cm^-3	10⁸ cm^-3
Mass	1-100 M_sun	10-1000 M_sun

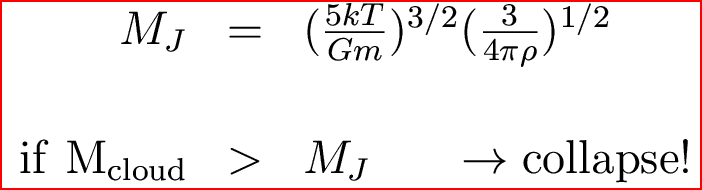
And the Jeans mass is given by:

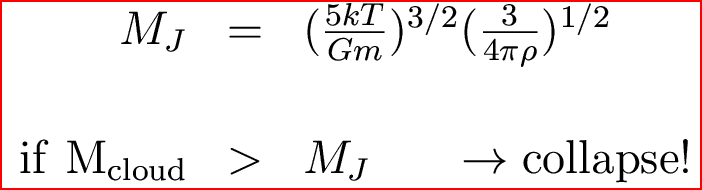
So plugging in numbers, we find that

Diffuse HI cloud: M_J ~ 1500 M_sun - stable.
Molecular cloud core: M_J ~ 15 M_sun - unstable!

So deep inside molecular clouds (the molecular clouds themselves may be 10⁶ - 10⁷ M_sun), the cores are collapsing to form stars. How does this collapse proceed?

Gravitational Free Fall

Early on in the collapse, the cloud is optically thin (it has a low density, so energy can escape easily without being absorbed). Since the energy of collapse is immediately radiated away, the cloud won't heat up -- we call this an isothermal collapse.

How fast does this collapse happen? Let's do a "back of the envelope" calculation.

Consider a particle somewhere inside the cloud. What is the gravitational acceleration it feels pulling it inwards?

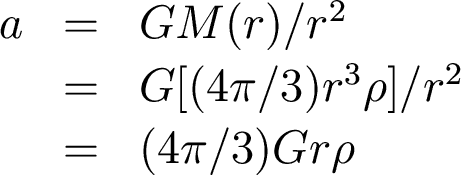
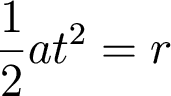
If it starts initially at rest, then (if acceleration is constant) it will reach the center when

So, solving for t,

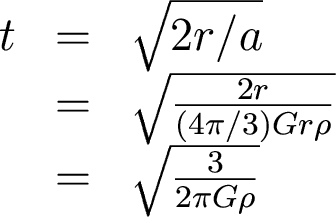
Now, since this is just a crude calculation, we can say that sqrt(3/2pi) = 0.7 = 1, so that we have an expression for the free fall time:

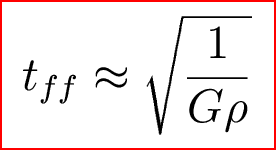
which is good to within a factor of two or so.

Note that the free-fall time depends only on density, not radius.

So how fast does the molecular cloud core collapse? Since it is mostly hydrogen,

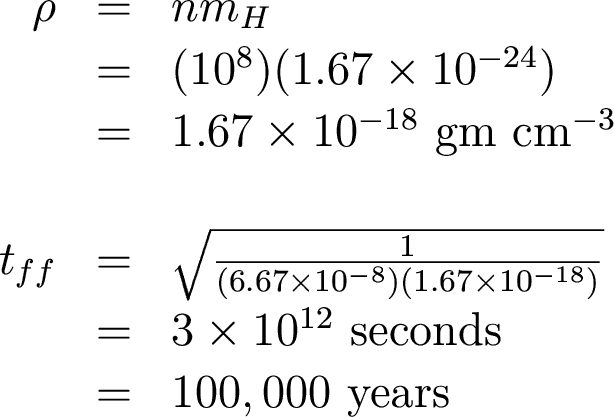
Fast! (by astronomical standards, anyway...)

Fragmentation

Of course this is a simplification -- a single cloud does not collapse down to r=0. What happens to complicate the collapse?

As the cloud collapse, density rises. Since the collapse is isothermal, a rising density means the Jeans mass of the cloud is falling, so small pieces of the cloud start to collapse on their own. A rising density also means a declining free fall time, so these small dense clumps collapse faster than the overall cloud.

Instead of one giant cloud undergoing a monolithic collapse, the cloud fragments into small collapsing pieces.

So what stops this fragmentation?

The transition to adiabatic collapse

As the density rises, the opacity rises. At some point during the collapse and fragmentation process, the opacity rises high enough that the energy created during the collapse is absorbed within the star itself -- it begins to heat up. Since the energy is not lost from the cloud, we call this an adiabatic collapse.

Higher temperature means higher pressures (the ideal gas law), which halt the free collapse of the star. Since the cloud absorbs all the gravitational energy of collapse, it heats up, and it starts to act like a blackbody.

At what mass does this happen? We can balance the rate of energy loss through gravitational collapse to the rate at which the cloud radiates blackbody energy, and, solving for the mass (see pp 454-455), we find M ~ M_sun. In other words, collapse halts when the fragment masses reach star-like masses. Protostars!