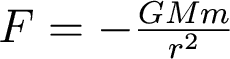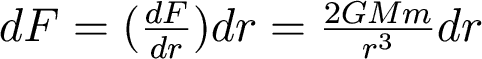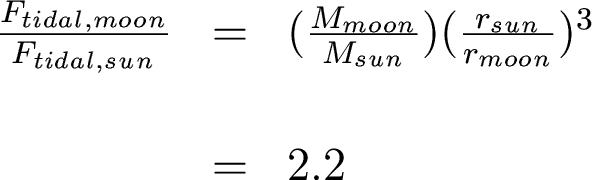Gravitational Tides
Look closely at the gravitational
force acting on a moon as it orbits its planet:
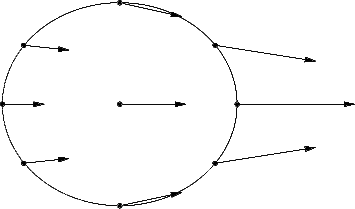 If we subtract the center of mass force, we see the differential
force acting on it:
If we subtract the center of mass force, we see the differential
force acting on it:
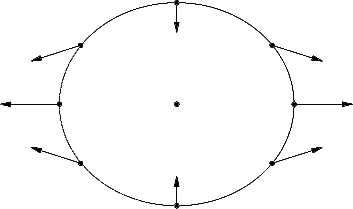
So gravity "stretches"
and "squashes" a moon!
Let's look at this mathematically. The force of gravity
is:
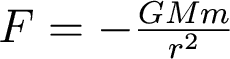 So the differential force
(also called the tidal force) across
a distance dr is
So the differential force
(also called the tidal force) across
a distance dr is
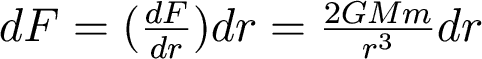 Note that
Note that
-
the tidal force is proportional to the mass of the primary
(M)
-
the tidal force is inversely proportional to the distance
cubed.
Note also that it works both ways -- the moon also stretches
the planet!
Why is it called a tidal force?
What is stronger on the Earth, the tidal force from the
moon or the tidal force from the Sun?
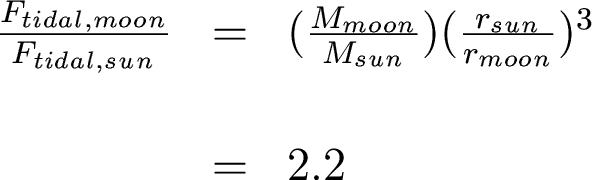 So the moon exerts a stronger force, but the Sun's tidal
force can be significant. Hence the concept of spring
tides and neap tides:
So the moon exerts a stronger force, but the Sun's tidal
force can be significant. Hence the concept of spring
tides and neap tides:
-
Spring Tides: Sun
and Moon in alignment; tidal forces add. Big
tides!
-
Neap Tides: Sun
and Moon 90 degrees apart; tidal forces counteract. Small
tides.
Remember: Tides are not merely a water effect! The Earth's
surface also has tidal bulges, about 10cm in height. And the moon has an
even greater tidal bulge -- 20m high.
Thought experiment: What
happens when you keep squeezing and stretching a piece of silly putty? What
does this have to do with tides?